² ² a ² − b ² a. The tower is 150 m tall and the distance from the top of the tower to the centre of the hyperbola is.
Equation Of Parabola Ellipse And Hyperbola. X 2 /a 2 + y 2 /b 2 = 1; But, if we examine a parabola in relation to its focal point (focus) and directrix, we can determine more information about the parabola.
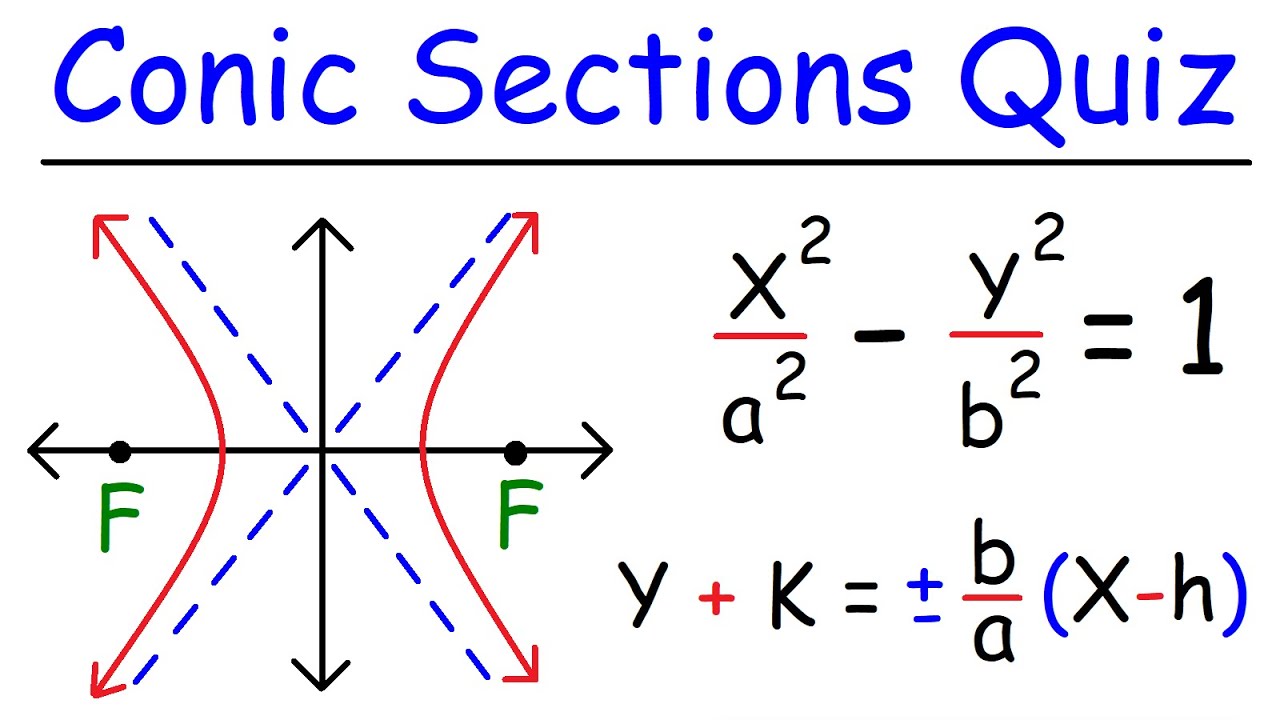
Find the Center, Foci, Vertices, and Asymptotes of a From youtube.com
X 2 +y 2 =a 2; Deriving the polar equation from the cartesian equation A conic section (or simply conic) is a curve acquired as the intersection of the surface of a cone with a plane.
Find the Center, Foci, Vertices, and Asymptotes of a
The circle is a type of ellipse and is from time to time viewed to be a fourth kind of conic section. Rxcos ,θ= the equation for the ellipse can also be written as (2) ( ) r a e ex e x x = − −= −1. 3.5 parabolas, ellipses, and hyperbolas 50 define f,(x) = sin x + 4 sin 3x + f sin 5x + (n terms). There are three types of conic sections are the hyperbola, the parabola, and the ellipse.
Source: slideshare.net
The tower is 150 m tall and the distance from the top of the tower to the centre of the hyperbola is half the distance from the base of the tower to the centre of the hyperbola. Here is how you distinguish the various conic sections from the coefficients in the general equation: Since j of = p, from 11.18.
Source: slideserve.com
² ² a ² − b ² a. Conic sections can be generated by using. For a parabola, the value of eccentricity is 1. #aneb# but a and b both have different signs. The equation x2 + 2y2 = 36 represents which conic section?
Source: slideserve.com
The tower is 150 m tall and the distance from the top of the tower to the centre of the hyperbola is half the distance from the base of the tower to the centre of the hyperbola. The equation x2 + 2y2 = 36 represents which conic section? An ellipse if e < 1. For a circle, the value of.
Source: youtube.com
The equation x2 + 2y2 = 36 represents which conic section? Conic sections can be generated by using. Your email address will not be published. And, of course, these remain popular equation forms of a parabola. Y = ax2 + bx + c from your study of quadratics.
Source: youtube.com
Y 2 =4ax when a>0; X 2 /a 2 + y 2 /b 2 = 1; Directrix for any point on the ellipse, its distance from the focus is. Your email address will not be published. Y = ax2 + bx + c from your study of quadratics.
Source: study.com
This playlist features a variety of videos on the topic of the equation of parabolas, ellipses, and hyperbolas. #aneb# but a and b both have different signs. \displaystyle p p is any point on the ellipse, p f + p f ′ = 2 a. For an ellipse, the value of eccentricity is equal to: The equation x2 + 2y2.
