Graph & features of ellipses. _ _6 + _ 4 = 1 parabola
Equation Of Ellipse And Circle. For a ≥ b ≥ 0 , eliminating the square. The circle is a special case of the ellipse where a=b=r, in the equation of the ellipse.
Determining What Type of Conic Section from General Form From youtube.com
If they have the same sign but different values the. The distance between any point on the circle and its center is constant, which is known as the radius. How many arcs does an ellipse have?
Determining What Type of Conic Section from General Form
Implementing the above conditions, i.e., when a = b. Implementing the above conditions, i.e., when a = b. X 2 /b 2 +y 2 /b 2 =1. Define b by the equations c 2 = a 2 − b 2 for an ellipse and c 2 = a 2 + b 2 for a hyperbola.
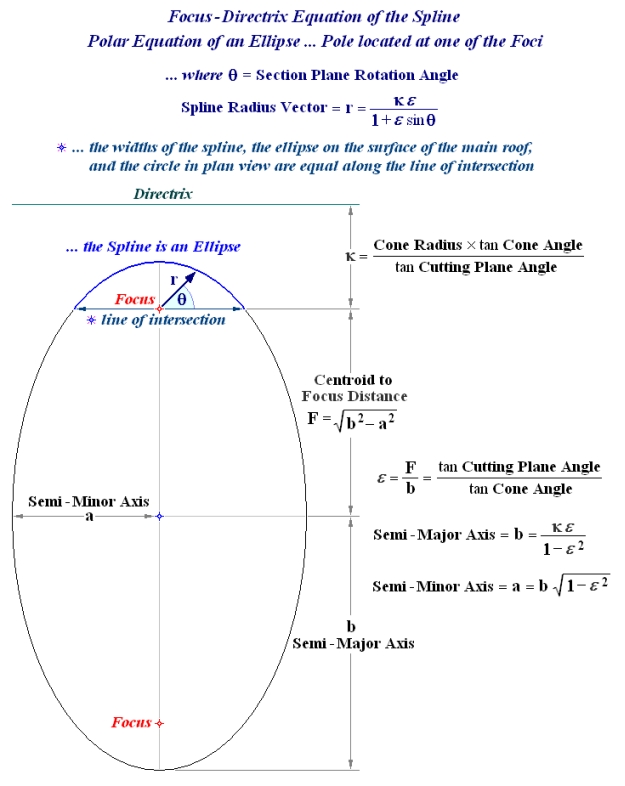Source: geocities.ws
If they have the same sign but different values the. The vertices are (±a, 0) and the foci (±c, 0). The points of intersection of the ellipse and the circle are. State whether the graph of each equation is a circle, parabola, or ellipse. (x−h)2 a2 + (y−k)2 b2 =1 ( x − h) 2 a 2 + ( y.
Source: youtube.com
The points of intersection of the ellipse and the circle are. The circle and ellipse do not intersect. ¯ mf1 + ¯ mf2 = √(x + c)2 + y2 + √(x − c)2 + y2 = 2a. State whether the graph of each equation is a circle, parabola, or ellipse. The standard form for the equation of the ellipse is:
Source: youtube.com
An ellipse is a conic section, formed by the intersection of a plane with a right circular cone. ¯ mf1 + ¯ mf2 = √(x + c)2 + y2 + √(x − c)2 + y2 = 2a. General equation of an ellipse (x h)2 a2 + (y k)2 b2 = 1 center at (h;k) vertices at (h +a;k), (h a;k),.
Source: youtube.com
Center and radii of an ellipse. (the definition of e can also be formulated in terms of lines Since a = b in the ellipse below, this ellipse is actually a circle whose standard form equation is x² + y² = 9 graph of ellipse from the equation the problems below provide practice creating the graph of an ellipse from.
Source: youtube.com
¯ mf1 + ¯ mf2 = √(x + c)2 + y2 + √(x − c)2 + y2 = 2a. Figure illustrates possible solution sets for a system of equations involving a circle and an ellipse. The circle and ellipse are tangent to each other, and intersect at exactly one. Ellipse has two foci, which are at the either ends. If.
