0 0 sin sin 1 cos lim 1 lim 0 lim 0 x x x x x x − −∞ −x x x A definite integral is used to compute.
Differentiation And Integration Table Pdf. Integrals and their elementary properties including some techniques of integration. A definite integral is used to compute the area under the curve these are some of the most frequently encountered rules for differentiation and integration.
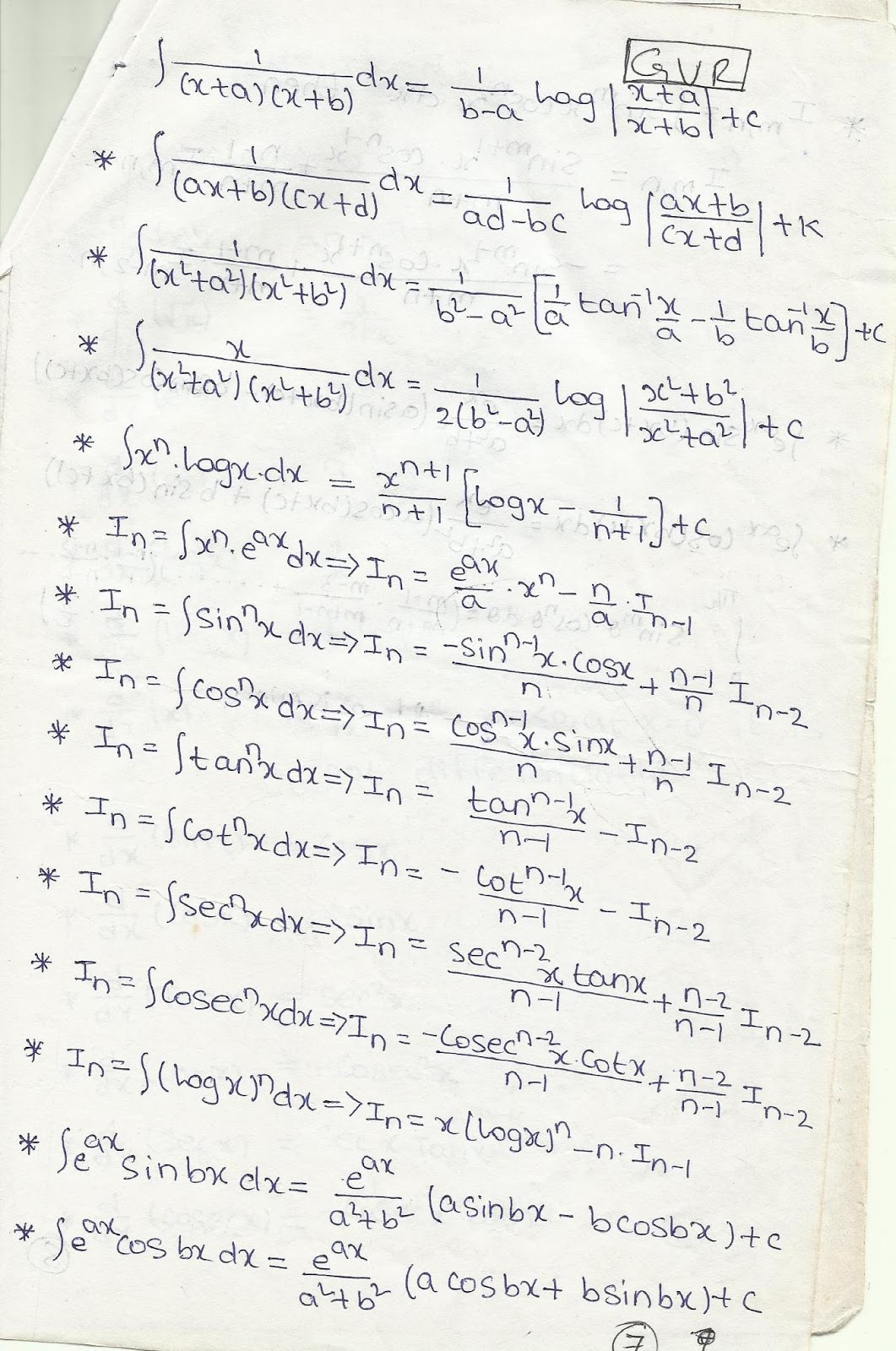CBSE Class 12 Maths Notes Indefinite Integrals Maths From pinterest.com
Basic differentiation rules basic integration formulas derivatives and integrals © houghton mifflin company, inc. Integration formulas y d a b x c= + −sin ( ) a is amplitude b is the affect on the period (stretch or shrink) c is vertical shift (left/right) and d is horizontal shift (up/down) limits: (a) the power rule :
CBSE Class 12 Maths Notes Indefinite Integrals Maths
©2005 be shapiro page 3 this document may not be reproduced, posted or published without permission. U ddx {(x3 + 4x + 1)3/4} = 34 (x3 + 4x + 1)−1/4.(3x2 + 4)d dx {u} = 12 u.u d dx { 2 − 4x2 + 7x5} = 1 2 2 − 4x2 + 7x5 (−8x + 35x4) d dx {c} = 0 , c is a constant ddx {6} = 0 , since ≅ 3.14 is a constant. The difference between differentiation and integration is that differentiation is used to find out the instant rates of change and the slopes of curves, whereas if you need to calculate the area under curves then make use of integration. A definite integral is used to compute the area under the curve these are some of the most frequently encountered rules for differentiation and integration.
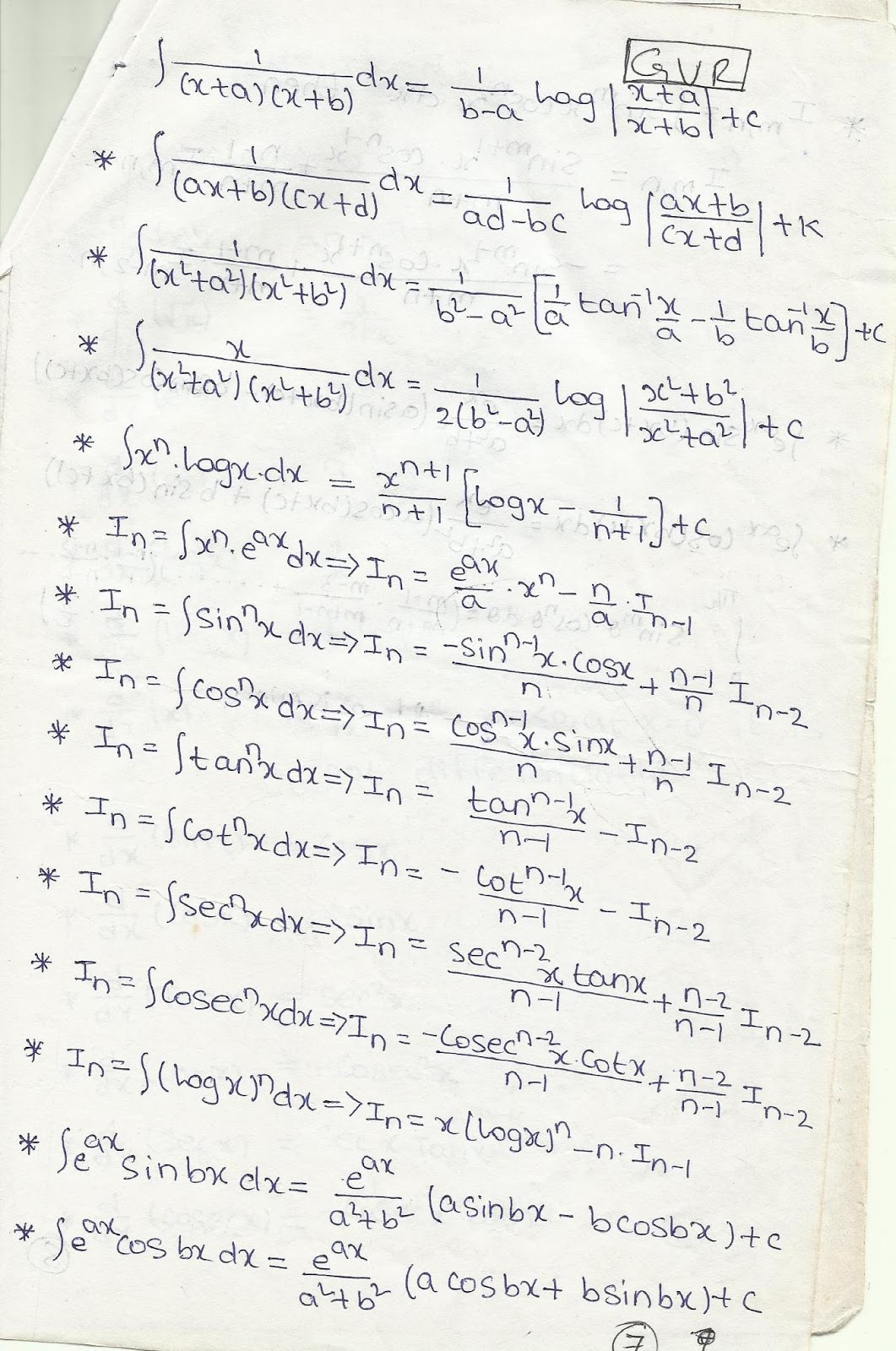Source: enggmathsworld.blogspot.com
Constant multiple rule [ ]cu cu dx d = ′, where c is a constant. Integrals and their elementary properties including some techniques of integration. If we compare differentiation and integration based on their properties: U substitution given (( )) ( ) b a ∫ f g x g x dx′ then the substitution u gx= ( ) will convert.
Source: elecengworld1.blogspot.com
1.1 motivation the primary issue in differentiation is the noise corruption. If a term in your choice for yp happens to be a solution of the homogeneous ode corresponding to (4), multiply this term by x (or by x 2 if this solution corresponds to a double root of the Standard integration techniques note that all but the first one.
Source: mpec.sc.mahidol.ac.th
U inverse trig function (sin ,arccos , 1 xxetc) logarithmic functions (log3 ,ln( 1),xx etc) algebraic functions (xx x3,5,1/, etc) trig functions (sin(5 ),tan( ),xxetc) Common derivatives and integrals provided by the academic center for excellence 1 reviewed june 2008 common derivatives and integrals derivative rules: The difference between differentiation and integration is that differentiation is used to find out.
Source: pinterest.com
Quotient rule v2 vu uv v u. Common derivatives and integrals provided by the academic center for excellence 1 reviewed june 2008 common derivatives and integrals derivative rules: If a term in your choice for yp happens to be a solution of the homogeneous ode corresponding to (4), multiply this term by x (or by x 2 if this solution.
Source: byjus.com
Functions ∫sin cosxdx x= − ∫cos sinxdx x= − sin sin22 1 2 4 x ∫ xdx x= − cos sin22 1 2 4 x ∫ xdx x= + sin cos cos3 31 3 ∫ xdx x x= − cos sin sin3 31 3 ∫ xdx x x= − ln tan sin 2 dx x xdx x ∫= Table of.
